गणित पर आधारित - जादुई संख्या पहेली (पैटर्न) हल करने की ट्रिक || Jadui sankhya paheli
गणित विषय में विद्यार्थियों को पैटर्न के अंतर्गत जादुई वर्ग पहेली की जानकारी दी जाती है। वर्ग पहेलियाँ कई तरह की होती है, जिनमें निम्न पहेलियाँ महत्वपूर्ण हैं।
(1) जादुई वर्ग पहेली- इस तरह की पहेली ऐसी होती है जिसमें कुल 9 वर्ग बने होते हैं। नीचे उदाहरण दिए गए हैं-
| A | B | C |
|---|---|---|
| H | I | D |
| G | F | E |
उक्त वर्ग में A से लेकर H तक अंग्रेजी लेटर्स लिखे गए हैं। इससे एक सूत्र का हम नीचे निर्माण करेंगे।
HEB CIG FAD
हेब सिग फैड
अब क्रमागत संख्याओं को कहीं से भी प्रारंभ करते हुए, उदाहरण के लिए 3 से 11 तक 9 संख्याओं को H से D तक निम्न प्रकार सूत्र में रखेंगे-
H E B C I G F A D
3,4,5, 6,7,8, 9,10,11
अब उक्त संख्याओं को वर्ग में जो लेटर जिस वर्ग में आया है उसे रखेंगे। जैसे- H के स्थान पर 3, E के स्थान पर 4, B के स्थान पर 5, C के स्थान पर 6, I के स्थान पर 7, G के स्थान पर 8, F के स्थान पर 9, A के स्थान पर 10, D के स्थान पर 11 रखेंगे।
| 10 | 5 | 6 |
|---|---|---|
| 3 | 7 | 11 |
| 8 | 9 | 4 |
उक्त वर्ग में आप देखेंगे आड़ा, खड़ा, तिरछा किसी भी तरह से 3 अंकों का जोड़ किया जाए तो जोड़ समान आता है। जैसे उक्त वर्ग में जोड़ किसी भी तरह किया जाए 21 आता है।
(2) जादुई तिकोन- इस तरह की पहेली ऐसी होती है जिसमें कुल 6 खण्ड बने होते हैं। नीचे उदाहरण दिए गए हैं-
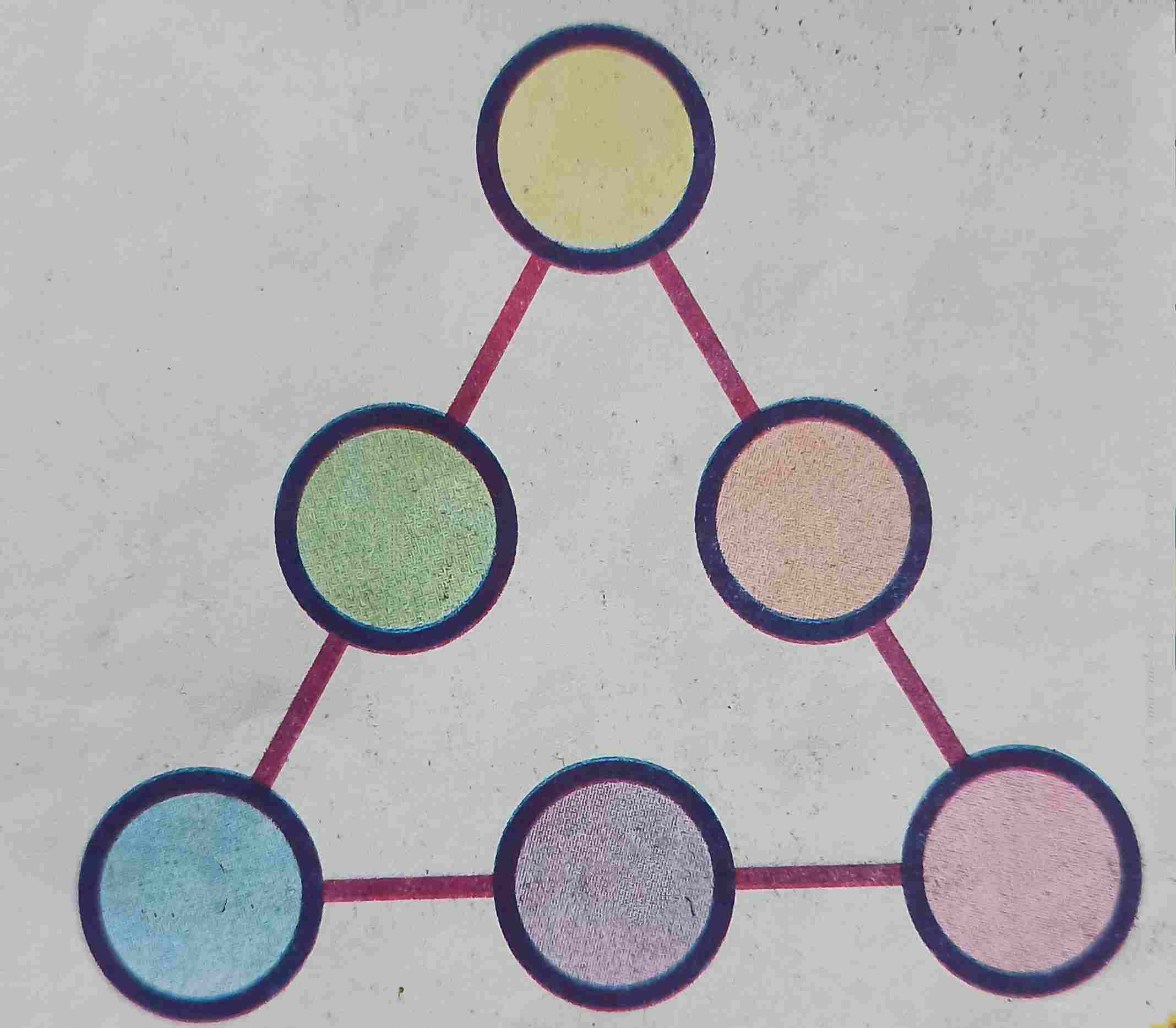
उक्त तिकोन में निम्नानुसार A से लेकर F तक अंग्रेजी लेटर्स लिखे गए हैं।
| A | ||
|---|---|---|
| F | B | |
| E | D | C |
इससे एक सूत्र का हम नीचे निर्माण करेंगे।
CFE BAD
सिफे बैड
उक्त सूत्र में किन्ही भी क्रमागत 6 संख्याओं को (उदाहरण के लिए 1 से 6) निम्नानुसार लिखेंगे।
C F E B A D
1, 2,3, 4,5,6
अब उक्त संख्याओं को बाक्स में जो लेटर जिस बाक्स में आया है उसे रखेंगे। जैसे- C के स्थान पर 1, F के स्थान पर 2, E के स्थान पर 3, B के स्थान पर 4, A के स्थान पर 5 और D के स्थान पर 6 रखेंगे।
| 5 | ||
|---|---|---|
| 2 | 4 | |
| 3 | 6 | 1 |
उक्त त्रिकोण में प्रत्येक पंक्ति को जोड़ने पर योगफल सामान आता है। यहाँ आप योग करेंगे तो योगफल प्रत्येक पंक्ति का 10 आएगा।
इसी तरह से उक्त त्रिकोण में यदि प्रत्येक पंक्ति का योगफल 9 आए तो इस हेतु अलग तरह के सूत्र का प्रयोग करना होगा।
C A E F D B
1, 2,3, 4,5,6
अब उक्त संख्याओं को बाक्स में जो लेटर जिस बाक्स में आया है उसे रखेंगे। जैसे- C के स्थान पर 1, A के स्थान पर 2, E के स्थान पर 3, F के स्थान पर 4, D के स्थान पर 5 और B के स्थान पर 6 रखेंगे।
| 3 | ||
|---|---|---|
| 4 | 5 | |
| 2 | 6 | 1 |
उक्त त्रिकोण में प्रत्येक पंक्ति को जोड़ने पर योगफल सामान आता है। यहाँ आप योग करेंगे तो योगफल प्रत्येक पंक्ति का 9 आएगा।
(3) सात अंकों का जादुई पैटर्न - इस तरह के पैटर्न ऐसा होता है जिसमें कुल 7 खण्ड बने होते हैं। नीचे उदाहरण दिए गए हैं-
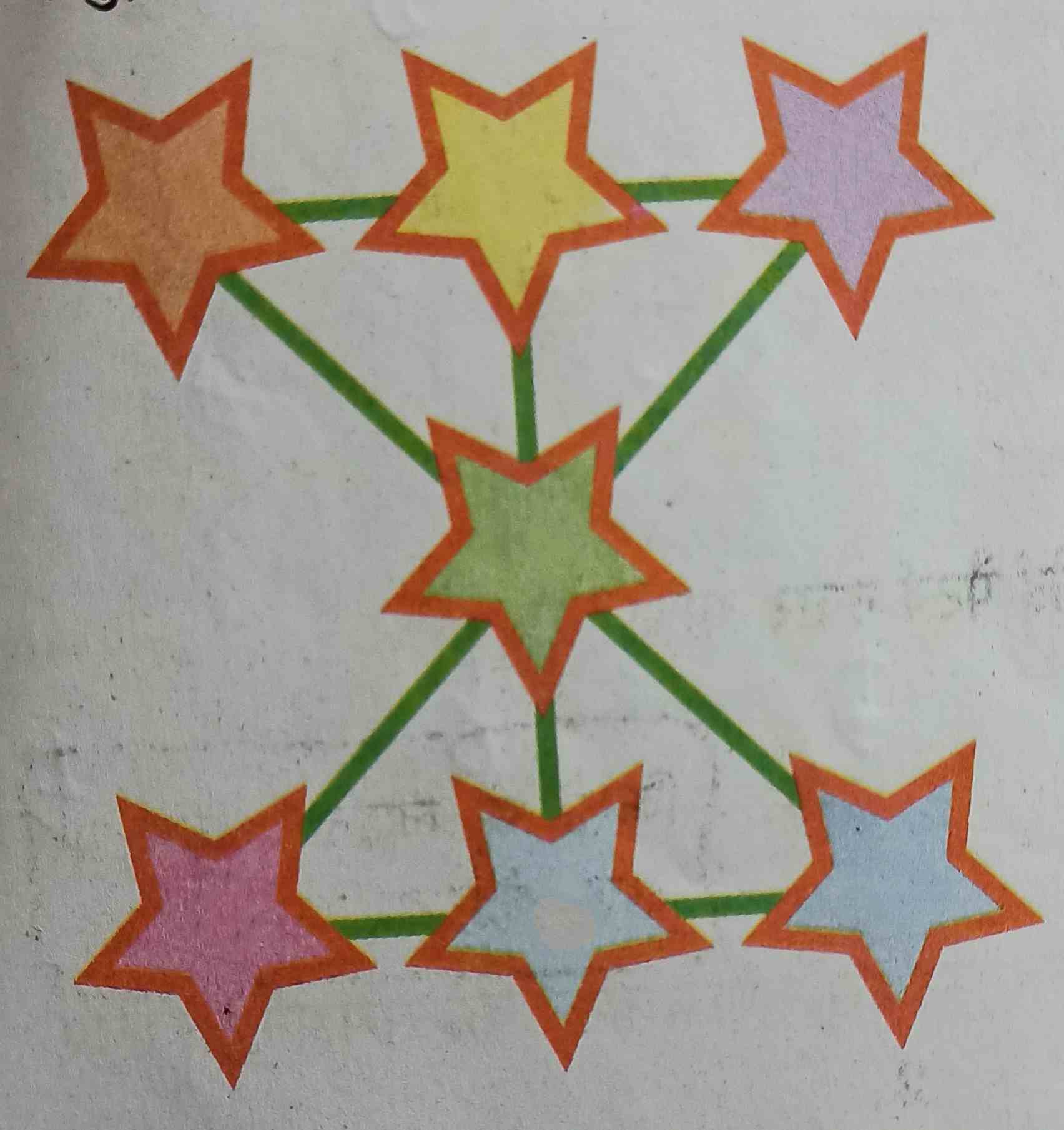
उक्त पैटर्न में निम्नानुसार A से लेकर F तक अंग्रेजी लेटर्स लिखे गए हैं।
| E | A | B |
|---|---|---|
| D | ||
| F | G | C |
उक्त पैटर्न में A से लेकर G तक अंग्रेजी लेटर्स लिखे गए हैं। इससे एक सूत्र का हम नीचे निर्माण करेंगे।
EABDFGC
अब क्रमागत संख्याओं को कहीं से भी प्रारंभ करते हुए, उदाहरण के लिए 1 से 7 तक कुल 7 संख्याओं को E से C तक निम्न प्रकार सूत्र में रखेंगे-
E A B D F G C
1, 2,3, 4,5, 6,7
अब उक्त संख्याओं को बाक्स में जो लेटर जिस बाक्स में आया है उसे रखेंगे। जैसे- E के स्थान पर 1, A के स्थान पर 2, B के स्थान पर 3, D के स्थान पर 4, F के स्थान पर 5, G के स्थान पर 6, C के स्थान पर 7 रखेंगे।
| 2 | 3 | 7 |
|---|---|---|
| 4 | ||
| 1 | 5 | 6 |
उक्त पैटर्न में आप देखेंगे आड़ा और तिरछा किसी भी तरह से 3 अंकों का जोड़ किया जाए तो जोड़ समान आता है। जैसे उक्त वर्ग में जोड़ किसी भी तरह किया जाए 12 आता है।
इसी तरह से यदि 5 से 11 तक संख्याओं को E से C तक निम्न प्रकार सूत्र में रखेंगे-E A B D F G C
5, 6,7, 8,9,10,11
तो अब उक्त संख्याओं को बाक्स में जो लेटर जिस बाक्स में आया है उसे रखेंगे। जैसे- E के स्थान पर 5, A के स्थान पर 6, B के स्थान पर 7, D के स्थान पर 8, F के स्थान पर 9, G के स्थान पर 10, C के स्थान पर 11 रखेंगे।
| 6 | 7 | 11 |
|---|---|---|
| 8 | ||
| 5 | 9 | 10 |
अब आप उक्त पैटर्न में आड़ा और तिरछा 3 अंकों का जोड़ करे तो 24 आता है।
इन गणित के प्रकरणों 👇 के बारे में भी जानें।
1. संख्याओं के प्रकार- प्राकृत, पूर्ण, पूर्णांक, परिमेय
2. भिन्न की समझ
3. विमा या आयाम क्या है? द्विविमीय या द्विआयामी एवं त्रिविमीय या त्रिआयामी वस्तुओं की अवधारणा
4. शून्य का गुणा, शून्यान्त संख्याओं का गुणा, गुण्य, गुणक एवं गुणनफल
5. भाग संक्रिया- भाग के घटक- भाज्य भाजक भागफल और शेष
(Watch video for related information)
आशा है, उपरोक्त जानकारी उपयोगी एवं महत्वपूर्ण होगी।
(I hope the above information will be useful and important. )
Thank you.
लेखक
(Writer)
infosrf.com
पाठकों की टिप्पणियाॅं (0)
Leave a reply
You may also like
National Mathematics Day - 22 December (राष्ट्रीय गणित दिवस) : श्रीनिवास रामानुजन की विरासत और गणितीय संकल्पना
महान गणितज्ञ रामानुजन का योगदान और गणित के अनछुए पहलू
Read more
गणित और ज्योतिष में 1 से 9 तक के अंकों का महत्व | 1 से 9 अंकों विश्लेषण, उपयोगिता और आध्यात्मिक महत्व की समन्वित प्रस्तुति
यह लेख अंक 1 से 9 तक के गणितीय महत्व के साथ-साथ उनके ज्योतिषीय और आध्यात्मिक पहलुओं का समग्र विश्लेषण प्रस्तुत करता है। प्रत्येक अंक की विशेषताओं को वैज्ञानिक एवं धार्मिक दृष्टिकोण से समझाते हुए, यह संख्याओं की बहुआयामी भूमिका को उजागर करता है।
Read more
इकाई, दहाई से लेकर शंख, दशशंख और ब्रह्मसंख्या (अनंत) तक की प्राचीन भारतीय गणना प्रणाली: विशाल संख्याओं की विलक्षण अवधारणा
भारत की प्राचीन गणनात्मक परंपरा में संख्याओं की अद्वितीय श्रेणी — जहाँ इकाई से शुरू होकर संख्याएं करोड़, खर्ब, नील, पद्म, शंख, दशशंख से होते हुए अनंत तक विस्तार पाती हैं, जो गणितीय चेतना और दार्शनिक गहराई को दर्शाती है।
Read more
